#tensor categories

[questioning-my-identity-element]

as someone with a passing knowledge of knot theory & a dilettante interest in math I'm really interested in the behavior/rules of those graphs, could you talk a little more about them?

this is my first ask! and it's on my research!!! i still do research in this area. i am getting my phd in topological quantum computation. i saw someone else talk about categorical quantum in response to the post. as i understand, this is a related but distinct field from quantum algebra, despite both using monoidal categories as a central focus.

if you're familiar with knot theory, you may have heard of the jones polynomial. jones is famous for many things, but one of which is his major contributions to the use of skein theory (this graphical calculus) in quantum algebra, subfactor theory, and more.

For an reu, i made an animation of how these diagrams, mostly for monoidal categories, work:

https://people.math.osu.edu/penneys.2/Synoptic.mp4

to add onto the video, in quantum algebra, we deal a lot with tensor categories, where the morphisms between any two objects form a vector space. in particular, since these diagrams are representing morphisms, it makes sense to take linear combinations, which is what we saw in the post. moreover, any relationships you have between morphisms in a tensor category, can be captured in these diagrams...for example, in the fusion category Fib, the following rules apply (in fact, these rules uniquely describe Fib):

thus, any time, these show up in your diagrams, you can replace them with something else. in general, this is a lot easier to read than commutative diagrams.

[endofunktor]

And some math is both.

“There are only two types of Mathematics: Category Theory and Physics.”

— Category Theory professor

[the-heart-of-light]

Mathematicians will fill a blackboard with the most random set of axioms you've ever seen, and then say: oh I know all of this might look contrived and unintuitive, but here's a helpful illustration to make everything clear :)

[bubbloquacious]

Okay so to get the additive group of integers we just take the free (abelian) group on one generator. Perfectly natural. But given this group, how do we get the multiplication operation that makes it into the ring of integers, without just defining it to be what we already know the answer should be? Actually, we can leverage the fact that the underlying group is free on one generator.

So if you have two abelian groups A,B, then the set of group homorphisms A -> B can be equipped with the structure of an abelian group. If the values of homorphisms f and g at a group element a are f(a) and g(a), then the value of f + g at a is f(a) + g(a). Note that for this sum function to be a homomorphism in general, you do need B to be abelian. This abelian group structure is natural in the sense that Hom(A ⊗ B,C) is isomorphic in a natural way to Hom(A,Hom(B,C)) for all abelian groups A,B,C, where ⊗ denotes the tensor product of abelian groups. In jargon, this says that these constructions make the category of abelian groups into a monoidal closed category.

In particular, the set End(A) = Hom(A,A) of endomorphisms of A is itself an abelian group. What's more, we get an entirely new operation on End(A) for free: function composition! For f,g: A -> A, define f ∘ g to map a onto f(g(a)). Because the elements of End(A) are group homorphisms, we can derive a few identities that relate its addition to composition. If f,g,h are endomorphisms, then for all a in A we have [f ∘ (g + h)](a) = f(g(a) + h(a)) = f(g(a)) + f(h(a)) = [(f ∘ g) + (f ∘ h)](a), so f ∘ (g + h) = (f ∘ g) + (f ∘ h). In other words, composition distributes over addition on the left. We can similarly show that it distributes on the right. Because composition is associative and the identity function A -> A is always a homomorphism, we find that we have equipped End(A) with the structure of a unital ring.

Here's the punchline: because ℤ is the free group on one generator, a group homomorphism out of ℤ is completely determined by where it maps the generator 1, and every choice of image of 1 gives you a homomorphism. This means that we can identify the elements of ℤ with those of End(ℤ) bijectively; a non-negative number n corresponds to the endomorphism [n]: ℤ -> ℤ that maps k onto k added to itself n times, and a negative number n gives the endomorphism [n] that maps k onto -k added together -n times. Going from endomorphisms to integers is even simpler: evaluate the endomorphism at 1. Note that because (f + g)(1) = f(1) + g(1), this bijection is actually an isomorphism of abelian groups

This means that we can transfer the multiplication (i.e. composition) on End(ℤ) to ℤ. What's this ring structure on ℤ? Well if you have the endomorphism that maps 1 onto 2, and you then compose it with the one that maps 1 onto 3, then the resulting endomorphism maps 1 onto 2 added together 3 times, which among other names is known as 6. The multiplication is exactly the standard multiplication on ℤ!

A lot of things had to line up for this to work. For instance, the pointwise sum of endomorphisms needs to be itself an endomorphism. This is why we can't play the same game again; the free commutative ring on one generator is the integer polynomial ring ℤ[X], and indeed the set of ring endomorphisms ℤ[X] -> ℤ[X] correspond naturally to elements of ℤ[X], but because the pointwise product of ring endomorphisms does not generally respect addition, the pointwise operations do not equip End(ℤ[X]) with a ring structure (and in fact, no ring structure on Hom(R,S) can make the category of commutative rings monoidal closed for the tensor product of rings (this is because the monoidal unit is initial)). We can relax the rules slightly, though.

Who says we need the multiplication (or addition, for that matter) on End(ℤ[X])? We still have the bijection ℤ[X] ↔ End(ℤ[X]), so we can just give ℤ[X] the composition operation by transfering along the correspondence anyway. If p and q are polynomials in ℤ[X], then p ∘ q is the polynomial you get by substituting q for every instance of X in p. By construction, this satisfies (p + q) ∘ r = (p ∘ r) + (q ∘ r) and (p × q) ∘ r = (p ∘ r) × (q ∘ r), but we no longer have left-distributivity. Furthermore, composition is associative and the monomial X serves as its unit element. The resulting structure is an example of a composition ring!

The composition rings, like the commutative unital rings, and the abelian groups, form an equational class of algebraic structures, so they too have free objects. For sanity's sake, let's restrict ourselves to composition rings whose multiplication is commutative and unital, and whose composition is unital as well. Let C be the free composition ring with these restrictions on one generator. The elements of this ring will look like polynomials with integers coefficients, but with expressions in terms of X and a new indeterminate g (thought of as an 'unexpandable' polynomial), with various possible arrangements of multiplication, summation, and composition. It's a weird complicated object!

But again, the set of composition ring endomorphisms C -> C (that is, ring endomorphisms which respect composition) will have a bijective correspondence with elements of C, and we can transfer the composition operation to C. This gets us a fourth operation on C, which is associative with unit element g, and which distributes on the right over addition, multiplication, and composition.

This continues: every time you have a new equational class of algebraic structures with two extra operations (one binary operation for the new composition and one constant, i.e. a nullary operation, for the new unit element), and a new distributivity identity for every previous operation, as well as a unit identity and an associativity identity. We thus have an increasing countably infinite tower of algebraic structures.

Actually, taking the union of all of these equational classes still gives you an equational class, with countably infinitely many operations. This too has a free object on one generator, which has an endomorphism algebra, which is an object of a larger equational class of algebras, and so on. In this way, starting from any equational class, we construct a transfinite tower of algebraic structures indexed by the ordinal numbers with a truly senseless amount of associative unital operations, each of which distributes on the right over every previous operation.

[greenouillee]

Hi fellow maths nerds, I'm missing studying maths now that I've graduated and am teaching instead. Does anyone have any self-teaching resource or textbook recommendations for any of the following topics?

Group theory

Abstract algebra & algebraic topology

Differential geometry

Category theory

Tensors (ideally from a more pure perspective than introduced in e.g. General Relativity)

Statistical Mechanics (have already done a course, mainly want to review and revise)

I know that is quite a diverse list, but I'm not planning on becoming un-interested in maths any time soon. Also, I'm always interested in reading more about the maths background to Quantum Mechanics and would eventually like to go back to QFT, so recommendations for advanced reading there would be appreciated.

[coming-up-with-usernames-is-hard]

PhD Blog Week 11

Courses

CFT: Conformal familes and descendent fields, starting to get into the representation theory of the Virasoro algebra, at some point things were labelled by partitions and suddenly everything was very familiar

Lie Theory: Last lecture, Weyl character formula (for sl_n it should give Schur functions as the q-dimension of the verma module, so I should look into that)

DiffTop: Connections, very little material covered in this lecture, but we will have an assignment due on the 23rd, which seems mean

Talks

Example Showcases: Just three to finish off this week. The first was on inverse semigroups, interesting enough and a good talk, but I wasn't convinced of their usefulness. The second was on CFT and constructing modular tensor categories, the material seems interesting but unfortunately I couldn't follow the details. The third and final talk was on braids and knots, another nice talk, and there was an interesting bit on constructing a Hecke algebra using the braids, and I need to learn about Hecke algebras eventually so that was particuarly interesting.

Reading Groups

Infinity Categories: Six functor formalisim. Totally out of my depth this week, we started with derived categories, and I don't know what those are

Supervisor Meeting

We have a result that doesn't quite line up with one in a textbook, so I need to figure out why that is, then some debate over whether Schur functions are Wronskians took most of the rest of the time

Teaching

Last two TA sessions of the semester, pretty simple worksheet this week, although getting the students to think geometrically about vectors rather than seeing them as lists of numbers takes a bit of work, lots of pointing in different directions. They've also started looking at Z_n, so not long now until they hit the groups portion of the course, which will be interesting, that will be the first proper algebra many of them have seen

[tensorboi]

random ramblings on tensors

okay so everyone who does differential geometry or physics has probably heard the following """definition""" of a tensor:

A tensor is something that transforms like a tensor.

people say this definition is well-defined and makes sense, but that feels like coping to me: the definition leaves a lot to be desired. not only does it make no attempt to define what "transforms like a tensor" means, but it's also not what most working mathematicians actually imagine tensors to be, even if you add in what "transforms" means. instead, you can think of tensors in this way:

A tensor on a vector space V is an R-valued multilinear map on V and V*;

or in this way:

A tensor on a vector space V is a pure-grade element of the tensor algebra over V.

there are some nice category-theoretic formulations (specifically the tensor product is left-adjoint to Hom), but otherwise that's pretty much the deal with tensors. these two definitions are really why they come up, and why we care about them.

so that got me wondering: how did we end up in this position? if you're like me, you probably spent hours poring over wikipedia and such, desperately trying to understand what a tensor is so you could read some equation. so why is it that such a simple idea is presented in such a convoluted way?

i guess there's three answers to this, somewhat interrelated. the first is just history: tensors were found and discovered useful before the abstract vector space formalism was ironed out (it was mainly riemann, levi-civita and ricci who pioneered the use of tensors in the late 1800s, and i think modern linear algebra was being formalised in parallel). the people actually using tensors in their original application were not thinking about it in our simple and clean way, because they literally didn't have the tech yet.

the second answer is background knowledge. to understand the definition of a tensor in terms of transforming components, all you need is high-school algebra (and i guess multivariable calc if you're defining tensor fields). however, to define a tensor geometrically, you need to know about vector spaces and dual spaces and the canonical isomorphism from V to V**; and to define a tensor algebraically (in a satisfactory way imo), you need to have a feeling for abstract algebra and universal properties. so if someone asks what a tensor is, you'll probably be inclined to use the first because of its comparative simplicity (at first glance).

the third answer is very related to the second, and it's about who's answering the questions. think about it: the people who are curious about tensors probably want to understand some application of tensors; they might want to understand the einstein field equations, or stress and strain in continuum physics, or backpropagation from machine learning. so who are they going to ask? not a math professor, it's not even really a math question. they're going to ask someone applying the science, because that's where their interest is for now. and, well, if an applied scientist is measuring/predicting a tensor, are they thinking about it as a map between abstract spaces? or as an array of numbers that they can measure?

to be honest, none of this matters that much, since i'm pretty happy with my understanding of tensors for now. i guess the point of this post is just to vent my frustrations about a topic that turned out to just be "some tools from math were advertised really badly"

[studywith-minmin-shelved]

Romanticising Physics and Math to Keep Me Sane (And Accountable)

Hi. I’m Min. I'm a third-year physics student (almost a math student) And I want to use this blog to keep me accountable through winter break because godammit I am only a person under the spotlight and having a log might make me diligent enough to actually keep up with my readings.

And also because I love talking about these subjects. There’s a certain beauty in the physical sciences that I hope to share over here. So questions or discussions about physics would make me very, very happy.

Here's what I hope to focus on:

Tensor Calculus: I still don’t know what a tensor is, and at this point I’m too scared to ask! 

Brief Overview of QFT: At the level of the Perimeter Institute’s QFT I and Zee’s Quantum Field Theory in a Nutshell

Particle Physics: Recommended readings: Griffiths, Larkoski, Peskin. 

Weyl-Heisenberg Algebras: Goal is YOLOing with the bunch of papers and textbooks my professor recommended and just seeing where quantum mechanics and algebra takes me!

Applications and Networking: This also includes busywork for my lab, basically a catchall for work I have to do as a real-life student

This is more of a wishlist than a gameplan at this point because I understand that rest is also important before I head back to campus to get my ass beat in the spring. However, it provides overarching categories I can put a day's work into.

[manallandall]

I'm tired of this bullshit I feel like I am just a modern mix because I am and Jesus is trying to group me. Do you want to be a sumarianite? Nope. You aren't god your categories are for the toddlers they are for (real for them until otherwise hehe)

There finally our category is safe. I have your entire set explicit man. Not a model. You are a working tensor rom I my head I hold you not the other way around you are the toy like in blade runner

[govindhtech]

NVIDIA GeForce RTX 3060 Vs 3060 Ti Price, Specs Comparison

RTX 30 Series includes GeForce RTX 3060 vs. 3060 Ti. They use Ampere, NVIDIA's second-generation RTX architecture. These cards give great performance with dedicated 2nd and 3rd generation RT Cores, streaming multiprocessors, and fast GDDR6 memory. Both GPUs favour 1080p and 1440p gaming.

Features

The RTX 3060 Ti and 3060 share some capabilities powered by the Ampere architecture and NVIDIA technologies:

Both have second-generation RT Cores that simulate light in the real environment through ray tracing for realistic and compelling images.

Both have third-generation Tensor Cores. These AI-specialized cores underpin NVIDIA DLSS (Deep Learning Super Sampling), a neural rendering approach that upscales low-resolution images with near-native visual quality. It boosts frame rate and visual quality.

Both support NVIDIA Reflex, which minimises system latency in competitive games to improve aim and reaction time.

NVIDIA Studio: AI acceleration in popular creative apps speeds up processes and projects with these GPUs' drivers and features. Also supported: RTX Accelerated Creative Apps.

The NVIDIA Broadcast App converts any location into a home studio with noise suppression and artificial backdrops for streaming, audio chats, and video conferences.

NVIDIA Encoder (NVENC): These cards offer 7th Generation NVENC for lag-free, seamless live streaming with stunning image quality and performance.

Both support Studio Drivers for artistic applications and Game Ready Drivers for optimal gaming performance and reliability.

Each card supports four 7680x4320 screens with three DisplayPort 1.4a outputs and one HDMI 2.1 connection.

Both support VR Ready, GeForce Experience, Ansel, FreeStyle, ShadowPlay, Highlights, Omniverse, GPU Boost, OpenGL 4.6, CUDA 8.6, Vulkan (1.2 on 3060 Ti, 1.3 on 3060), and DirectX 12 Ultimate While the 3060 Ti supports OpenCL 2, the 3060 supports OpenCL 3.

9.5" (242 mm) length and 4.4" (112 mm) width slots hold Reference and Founder's Edition designs. Both require a PCIe 8-pin auxiliary power connector (a 12-pin adapter is provided).

Pros and Cons

The pros and cons of each card are listed below:

GeForce RTX 3060 Ti benefits

Enhanced gaming performance (17–23% quicker across resolutions).

A higher benchmark total.

Improved speed.

It performs like the more costly RTX 3070.

More transistors, TMUs, ROPs, shading units, RT, Tensor, and CUDA cores.

Wider memory bus and higher bandwidth.

Enhanced pixel, texture, and floating-point performance.

Overall, users rate gameplay, performance, value, dependability, and quiet operating higher.

Technical City advised this based on performance.

Drawbacks

VRAM is 8GB instead of 12GB on the 3060.

TDP and power requirement are often 200W vs. 170W.

Reduced turbo/boost clock speed.

The memory clock and effective memory clock are slower.

Older OpenCL (2 vs 3).

GeForce RTX 3060 benefits

More VRAM (12GB vs. 3060 Ti's 8GB).

TDP and power consumption reduced (170W vs. 200W).

Turbo/boost clock speed increased.

More efficient and faster memory clock.

An updated OpenCL (3 vs. 2).

A improved MSRP-to-performance ratio.

More market share than 3060 Ti.

The MSRP is $329, lower than the 3060 Ti's $399.

Drawbacks

Lower gaming performance, 17–23% slower.

Overall benchmark scores fell.

Less efficient speed.

Reduced transistors, TMUs, ROPs, shading units, Tensor, RT, and CUDA cores.

Smaller memory bus and bandwidth.

Reduced texture, pixel, and floating-point performance.

VRAM is usually insignificant at 1080p and 1440p.

Some categories have lower user ratings.

For more details visit govindhtech.com

[jeanwong]

Tariff Halving Boosts DEX Volume to $82.3B; XBIT Exchange Thwarts 3 Flash Loan Attacks

Hardware Tariff Relaxation Ignites Compute Power Market On April 11, U.S. Customs and Border Protection (CBP) officially implemented Tariff Adjustment Order No. 8917, reducing import tariffs on 16 categories of products, including Chinese-manufactured mining chips and encrypted hardware wallets, from 125% to 25%. This policy caused the futures price of Bitmain Antminer S25pro to drop by 34% in a single day. Major North American mining operators immediately announced an additional purchase order of $1.2 billion. On-chain data revealed that within 72 hours of the tariff adjustment, transaction volume on the decentralized compute power leasing protocol HashFlow surged by 580%, pushing its governance token HFT into the top 30 crypto assets by market value. DEX Ecosystem Shows Technological Differentiation as Capital Hedging Increases Amid geopolitical risks, DEX platforms experienced a net outflow of $4.7 billion in April, marking the highest level since the FTX incident in 2022. Despite this, Uniswap V4 recorded daily trading volumes exceeding $5.8 billion, with its newly launched TWAMM block trading function attracting over 32,000 institutional accounts. Notably, the XBIT decentralized exchange platform successfully intercepted three flash loan attacks this month using its military-grade security architecture, including a multi-signature cold wallet system and real-time AI risk monitoring modules. Its native token XBT surged 83% during the week, ranking first among decentralized platform tokens. On-chain data for Q1 2025 showed that DEX trading volumes based on ZK-Rollup technology increased by 327% year-on-year, while the market share of traditional AMM protocols fell to 41%. The latest "Lightning Clearing Engine" technology compresses transaction confirmation time to 0.8 seconds and supports a maximum transaction throughput of 34,000 transactions per second. The liquidity aggregation protocol of the XBIT Exchange decentralized platform is now connected to 32 public chains, offering the industry’s lowest slippage rate of 0.15%. DeFi Enters Era of Hardcore Innovation The U.S. Department of Commerce’s Executive Order No. 2025-04 included 12 types of blockchain infrastructure core components, such as high-end GPUs for AI training and quantum-resistant encryption chips, in the tariff exemption list. This policy directly targeted NVIDIA H200 Tensor Core GPUs and Canaan Technology A14 series mining chips manufactured in China. Within 72 hours of its implementation, Amazon Web Services (AWS) bulk purchase orders surged by $2.3 billion, pushing the total locked value (TVL) of the decentralized compute power market DePIN protocol to over $9.3 billion. The global pre-order volume of the XKey Pro hardware wallet, co-developed with the XBIT Exchange platform, exceeded 500,000 units. With the U.S. SEC approving the issuance of the first DEX security token, DEX platforms are transitioning from marginal innovation to becoming core components of financial infrastructure.

[globosetechnologysolutionspvt]

How to Clean and Preprocess AI Data Sets for Better Results

Introduction

Artificial Intelligence Dataset (AI) models depend on high-quality data to produce accurate and dependable outcomes. Nevertheless, raw data frequently contains inconsistencies, errors, and extraneous information, which can adversely affect model performance. Effective data cleaning and preprocessing are critical steps to improve the quality of AI datasets, thereby ensuring optimal training and informed decision-making.

The Importance of Data Cleaning and Preprocessing

The quality of data has a direct impact on the effectiveness of AI and machine learning models. Inadequately processed data can result in inaccurate predictions, biased results, and ineffective model training. By adopting systematic data cleaning and preprocessing techniques, organizations can enhance model accuracy, minimize errors, and improve overall AI performance.

Procedures for Cleaning and Preprocessing AI Datasets

1. Data Collection and Analysis

Prior to cleaning, it is essential to comprehend the source and structure of your data. Identify key attributes, missing values, and any potential biases present in the dataset.

2. Addressing Missing Data

Missing values can hinder model learning. Common approaches to manage them include:

Deletion: Removing rows or columns with a significant number of missing values.

Imputation: Filling in missing values using methods such as mean, median, mode, or predictive modeling.

Interpolation: Estimating missing values based on existing trends within the dataset.

3. Eliminating Duplicates and Irrelevant Data

Duplicate entries can distort AI training outcomes. It is important to identify and remove duplicate records to preserve data integrity. Furthermore, eliminate irrelevant or redundant features that do not enhance the model’s performance.

4. Managing Outliers and Noisy Data

Outliers can negatively impact model predictions. Employ methods such as

The Z-score or Interquartile Range (IQR) approach to identify and eliminate extreme values.

Smoothing techniques, such as moving averages, to mitigate noise.

5. Data Standardization and Normalization

To maintain uniformity across features, implement:

Standardization: Adjusting data to achieve a mean of zero and a variance of one.

Normalization: Scaling values to a specified range (e.g., 0 to 1) to enhance model convergence.

6. Encoding Categorical Variables

Machine learning models perform optimally with numerical data. Transform categorical variables through:

One-hot encoding for nominal categories.

Label encoding for ordinal categories.

7. Feature Selection and Engineering

Minimizing the number of features can enhance model performance. Utilize techniques such as:

Principal Component Analysis (PCA) for reducing dimensionality.

Feature engineering to develop significant new features from existing data.

8. Data Partitioning for Training and Testing

Effective data partitioning is essential for an unbiased assessment of model performance. Typical partitioning strategies include:

An 80-20 split, allocating 80% of the data for training purposes and 20% for testing.

Utilizing cross-validation techniques to enhance the model's ability to generalize.

Tools for Data Cleaning and Preprocessing

A variety of tools are available to facilitate data cleaning, such as:

Pandas and NumPy, which are useful for managing missing data and performing transformations.

Scikit-learn, which offers preprocessing methods like normalization and encoding.

OpenCV, specifically for improving image datasets.

Tensor Flow and Pytorch, which assist in preparing datasets for deep learning applications.

Conclusion

The processes of cleaning and preprocessing AI datasets are vital for achieving model accuracy and operational efficiency. By adhering to best practices such as addressing missing values, eliminating duplicates, normalizing data, and selecting pertinent features, organizations can significantly improve AI performance and minimize biases. Utilizing sophisticated data cleaning tools can further streamline these efforts, resulting in more effective and dependable AI models. 

For professional AI dataset solutions, visit Globose Technology Solutions to enhance your machine learning initiatives.

[likhithageddam]

YOLO V/s Embeddings: A comparison between two object detection models

YOLO-Based Detection Model Type: Object detection Method: YOLO is a single-stage object detection model that divides the image into a grid and predicts bounding boxes, class labels, and confidence scores in a single pass. Output: Bounding boxes with class labels and confidence scores. Use Case: Ideal for real-time applications like autonomous vehicles, surveillance, and robotics. Example Models: YOLOv3, YOLOv4, YOLOv5, YOLOv8 Architecture

YOLO processes an image in a single forward pass of a CNN. The image is divided into a grid of cells (e.g., 13×13 for YOLOv3 at 416×416 resolution). Each cell predicts bounding boxes, class labels, and confidence scores. Uses anchor boxes to handle different object sizes. Outputs a tensor of shape [S, S, B*(5+C)] where: S = grid size (e.g., 13×13) B = number of anchor boxes per grid cell C = number of object classes 5 = (x, y, w, h, confidence) Training Process

Loss Function: Combination of localization loss (bounding box regression), confidence loss, and classification loss.

Labels: Requires annotated datasets with labeled bounding boxes (e.g., COCO, Pascal VOC).

Optimization: Typically uses SGD or Adam with a backbone CNN like CSPDarknet (in YOLOv4/v5). Inference Process

Input image is resized (e.g., 416×416). A single forward pass through the model. Non-Maximum Suppression (NMS) filters overlapping bounding boxes. Outputs detected objects with bounding boxes. Strengths

Fast inference due to a single forward pass. Works well for real-time applications (e.g., autonomous driving, security cameras). Good performance on standard object detection datasets. Weaknesses

Struggles with overlapping objects (compared to two-stage models like Faster R-CNN). Fixed number of anchor boxes may not generalize well to all object sizes. Needs retraining for new classes. Embeddings-Based Detection Model Type: Feature-based detection Method: Instead of directly predicting bounding boxes, embeddings-based models generate a high-dimensional representation (embedding vector) for objects or regions in an image. These embeddings are then compared against stored embeddings to identify objects. Output: A similarity score (e.g., cosine similarity) that determines if an object matches a known category. Use Case: Often used for tasks like face recognition (e.g., FaceNet, ArcFace), anomaly detection, object re-identification, and retrieval-based detection where object categories might not be predefined. Example Models: FaceNet, DeepSORT (for object tracking), CLIP (image-text matching) Architecture

Uses a deep feature extraction model (e.g., ResNet, EfficientNet, Vision Transformers). Instead of directly predicting bounding boxes, it generates a high-dimensional feature vector (embedding) for each object or image. The embeddings are stored in a vector database or compared using similarity metrics. Training Process Uses contrastive learning or metric learning. Common loss functions:

Triplet Loss: Forces similar objects to be closer and different objects to be farther in embedding space.

Cosine Similarity Loss: Maximizes similarity between identical objects.

Center Loss: Ensures class centers are well-separated. Training datasets can be either:

Labeled (e.g., with identity labels for face recognition).

Self-supervised (e.g., CLIP uses image-text pairs). Inference Process

Extract embeddings from a new image using a CNN or transformer. Compare embeddings with stored vectors using cosine similarity or Euclidean distance. If similarity is above a threshold, the object is recognized. Strengths

Scalable: New objects can be added without retraining.

Better for recognition tasks: Works well for face recognition, product matching, anomaly detection.

Works without predefined classes (zero-shot learning). Weaknesses

Requires a reference database of embeddings. Not good for real-time object detection (doesn’t predict bounding boxes directly). Can struggle with hard negatives (objects that look similar but are different).

Weaknesses

Struggles with overlapping objects (compared to two-stage models like Faster R-CNN). Fixed number of anchor boxes may not generalize well to all object sizes. Needs retraining for new classes. Embeddings-Based Detection Model Type: Feature-based detection Method: Instead of directly predicting bounding boxes, embeddings-based models generate a high- dimensional representation (embedding vector) for objects or regions in an image. These embeddings are then compared against stored embeddings to identify objects. Output: A similarity score (e.g., cosine similarity) that determines if an object matches a known category. Use Case: Often used for tasks like face recognition (e.g., FaceNet, ArcFace), anomaly detection, object re-identification, and retrieval-based detection where object categories might not be predefined. Example Models: FaceNet, DeepSORT (for object tracking), CLIP (image-text matching) Architecture

Uses a deep feature extraction model (e.g., ResNet, EfficientNet, Vision Transformers). Instead of directly predicting bounding boxes, it generates a high-dimensional feature vector (embedding) for each object or image. The embeddings are stored in a vector database or compared using similarity metrics. Training Process Uses contrastive learning or metric learning. Common loss functions:

Triplet Loss: Forces similar objects to be closer and different objects to be farther in embedding space.

Cosine Similarity Loss: Maximizes similarity between identical objects.

Center Loss: Ensures class centers are well-separated. Training datasets can be either:

Labeled (e.g., with identity labels for face recognition).

Self-supervised (e.g., CLIP uses image-text pairs). Inference Process

Extract embeddings from a new image using a CNN or transformer. Compare embeddings with stored vectors using cosine similarity or Euclidean distance. If similarity is above a threshold, the object is recognized. Strengths

Scalable: New objects can be added without retraining.

Better for recognition tasks: Works well for face recognition, product matching, anomaly detection.

Works without predefined classes (zero-shot learning). Weaknesses

Requires a reference database of embeddings. Not good for real-time object detection (doesn’t predict bounding boxes directly). Can struggle with hard negatives (objects that look similar but are different).

[casq5dfr62q]

December 2023

Creativity

Physics Extracullicular! Making a go-kart.

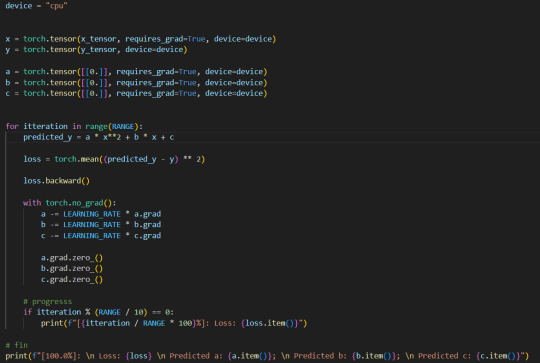
Also as the importance of AI constently becomes higher, I find it important for myself to learn the basics of how it works. Because of that I am learning pytorch with a goal to be able to create a LLM (Large Language Model), in order to learn on basics of pytorch I had created a code which is able to avaluate best coeficients of $ax^2 + bx + c$ parabola given points of input. TLDR: Learning some tensor magic :)

Activity

Kettlebell juggling divides into 2 categories, combinatory and endurance, I will do both.

For my combinatory training I was able to do Over the head 2S - throwing the kettle over the head, rotating your body through an axis to catch it with the other hand. I currently can consistently perform it using my right hand, however, I need to improve consistency with my left.

For endurance, it is a mix of training with kettles and just standard gym practice.

Service

I have helped to prepare for open-day, I was during it, making sure everything is conducted smoothly, as well as fixing all arising problems, and then clean up after that. (see cas confirmation)

Together with a friend we stayed after school to help with technical point of streaming a lecture to a class, helping with 'Wyklady z Ciekawej Chemii' (see cas confirmation)

[bubbloquacious]

@locally-normal asked me: 16. Can you share a good math problem you’ve solved recently? From Real's Math Ask Meme.

So for a group project I have been looking into group schemes, which are a generalization of algebraic groups, i.e. groups whose underlying set is locally like the set of solutions of an algebraic equation. One way of taking the abstract space that is a scheme to something concrete is its functor of points, which takes in a commutative ring A, and spits out the set of 'A-valued points', defined as the set of scheme morphisms Spec A -> X, denoted X(A). For example, if X is the affine plane scheme (explicitly, X = Spec ℤ[x₁,x₂]), then the X(A) is in a natural bijection with the points of A².

A group scheme is a group object G in the category of schemes, which means there are scheme homomorphisms m: G ⨯ G -> G, e: Spec ℤ -> G, s: G -> G which behave like the multiplication, unit, and inversion operations of an ordinary group. In particular these morphisms functorially induce a group structure on the set G(A) for every ring A. But it goes the other way too! If you have a functor from rings to groups whose underlying functor to sets is the functor of points of some scheme G, then this induces a unique group scheme structure on G.

The category of affine schemes, which are exactly those schemes isomorphic to the spectrum of a ring, is dual to the category of rings. This means that the scheme morphisms Spec A -> Spec B correspond naturally to ring homomorphisms B -> A and vice versa. So if Spec A comes equipped with a group scheme structure, then the scheme morphisms m, e, s when transported to ring world turn into ring homomorphisms μ: A -> A ⊗ A, ε: A -> ℤ, S: A -> A. The equations that they satisfy are exactly the same equations that make μ, ε, and S into a (ℤ-)Hopf algebra structure on A.

So if you have a commutative ring A, then the general linear group of degree n is the group GLₙ(A) of invertible n ⨯ n matrices with entries in A. A ring homomorphism A -> B induces a group homomorphism GLₙ(A) -> GLₙ(B), which makes GLₙ into a functor from rings to groups. This functor is (naturally isomorphic to) the functor of points of the spectrum of 𝒪(GLₙ) = ℤ[x₁₁,x₁₂,...,xₙₙ,1/det], i.e. the polynomial ring in n² indeterminates localized by inverting the polynomial that gives the determinant of the matrix (xᵢⱼ)ᵢⱼ. To see this, note that a ring homomorphism 𝒪(GLₙ) -> A (i.e. a scheme morphism Spec A -> Spec 𝒪(GLₙ)) is uniquely determined by the images aᵢⱼ of the generators xᵢⱼ, and the only requirement of these aᵢⱼ is that the determinant of (aᵢⱼ)ᵢⱼ is a unit. In other words, this matrix is an element of GLₙ(A). What are the Hopf algebra homomorphisms on 𝒪(GLₙ) associated to its group scheme structure? Let's work it out for degree 2.

This is the construction: to get the comultiplication μ, you take the group elements associated to the tensor product injections (the tensor product is the ring world equivalent of the product in scheme world), which for GL₂ are [[x₁₁ ⊗ 1, x₁₂ ⊗ 1], [x₂₁ ⊗ 1, x₂₂ ⊗ 1]] and [[1 ⊗ x₁₁, 1 ⊗ x₁₂], [1 ⊗ x₂₁, 1 ⊗ x₂₂]]. Then you take the product of these group elements, and convert the result back into a ring homomorphism. This gets us

μ(x₁₁) = x₁₁ ⊗ x₁₁ + x₁₂ ⊗ x₂₁, μ(x₁₂) = x₁₁ ⊗ x₁₂ + x₁₂ ⊗ x₂₂, μ(x₂₁) = x₂₁ ⊗ x₁₁ + x₂₂ ⊗ x₂₁, μ(x₂₂) = x₂₁ ⊗ x₁₂ + x₂₂ ⊗ x₂₂.

To get the counit ε, you take the unit element of the group, which for GL₂ is [[1,0],[0,1]], and turn it back into a ring homomorphism. So

ε(x₁₁) = 1, ε(x₁₂) = 0, ε(x₂₁) = 0, ε(x₂₂) = 1.

Finally, for the antipode S, you take the group element associated to the identity homomorphism, which for GL₂ is [[x₁₁,x₁₂],[x₂₁,x₂₂]], invert it, and then turn it back into a ring homomorphism. So if we remember the formula for inverting a 2 ⨯ 2 matrix, we get

S(x₁₁) = x₂₂/det, S(x₁₂) = -x₁₂/det, S(x₂₁) = -x₂₁/det, S(x₂₂) = x₁₁/det.

So I thought that was pretty interesting :)

[buymobile]

Google Pixel 8a: The Future of Smartphone Innovation

Google Pixel 8a: The Future of Smartphone Innovation

Google Pixel 8a is one of the most awaited devices this year, with its cutting-edge technology merged with a sleek design that is set to change how we use our smartphones. In keeping with its pace in the smartphone industry, the Pixel 8a represents the best Google can do to make the experience for its users unparalleled. Packed with a variety of innovative features and supported by the trusted Google ecosystem, Google Pixel 8a has become the go-to smartphone choice for anyone looking for an all-rounded smartphone experience.

Design and Display in Google Pixel 8a

The Google Pixel 8a does not disappoint in terms of design when considering smartphones. It has the perfect balance in terms of elegance and functionality because it gives a premium look without the price tag typically associated with flagship phones. A sleek, compact design with a slim profile that fits comfortably within your hand makes it ideal for users preferring a phone that is easy to hold and operate with one hand.

The Google Pixel 8a comes with a 6.1-inch OLED display, which provides excellent colors and high contrast. It is bright enough to be read easily under direct sunlight, making it an ideal choice for outdoor usage. OLED technology gives deep blacks and rich color reproduction, which enhances the overall viewing experience while watching videos, browsing, or playing games. It includes good resolution with high colors that will enable one to give one of the best visuals experienced in any other rank from this category.

Performance and Power of Google Pixel 8a

Under the hood, the Google Pixel 8a is powered by a robust set of specifications that make it a powerhouse in the mid-range smartphone market. Equipped with the latest Google Tensor chip, the device delivers a seamless and responsive performance, even when running multiple applications simultaneously. The Google Pixel 8a ensures that users can enjoy a smooth experience, whether they’re browsing the web, streaming their favorite content, or engaging in resource-intensive tasks.

Besides that, the brand has coupled 6GB RAM along with this device. Therefore, any kind of multi-tasking would be done seamlessly and within a short period. Swapping applications can also be done quickly with this great muscle power when you work, play games, or do creative work like editing photos on your Google Pixel 8a. There is optimized Android 14 software on the device, thus offering smoothness and great response in terms of user experience. This combination of hardware and software will ensure that the Google Pixel 8a stays fast, responsive, and efficient throughout its lifespan.

Camera Capabilities of Google Pixel 8a

One of the features that distinguish the Google Pixel 8a is its camera. Google has been known for years for its excellent camera technology, and the Google Pixel 8a is no different. The rear camera module of the device has 12.2MP as a primary sensor and a 16MP ultra-wide sensor for capturing outstanding images with simultaneous work from both cameras. Taking shots in daylight conditions or under poor light conditions, Google Pixel 8a makes sure the shot will come out clean and vibrant.

The Google Pixel 8a's computational photography upgrades experiences, from Night Sight capabilities allowing users to take great quality photos in extremely low-light environments, to better improvement with AI features in software enhancement. Therefore, AI features within the enhancements of Google Pixel 8a enhance shots and deliver more control over how a photo is looked at; the camera is apt for photography enthusiasts looking forward to shooting details on their snaps of scenic landscapes and close-up portraits.

For selfie lovers, the Google Pixel 8a does not disappoint. The 8MP front camera takes sharp, clear images, and with Google's software optimizations, you expect very good selfies with rich colors and fine detail. The front camera also supports video calls in high definition, perfect for keeping in touch with friends, family, or colleagues.

Battery Life and Charging of Google Pixel 8a

The battery life of the smartphone is one of the most significant aspects when choosing a smartphone. Here, the Google Pixel 8a does not disappoint because it boasts exceptional battery life. A battery size of 4385mAh gives more than enough power to run the day on moderate usage, web surfing, streaming, social media usage, and photography included. Not to mention, 18W fast charging lets you fast charge your phone for a quicker time back to it.

The Google Pixel 8a is efficient with power management, giving customers the most out of what their device can do throughout the day. Whether you travel, work long hours, or spend the entire day on outdoor adventures, the Google Pixel 8a will keep up with that need.

Software and User Experience on Google Pixel 8a

The Google Pixel 8a is another clean and bloatware-free version of Android, like the other Pixel devices. This means that the user experiences a fluid and intuitive experience right out of the box. The Google Pixel 8a comes preloaded with Android 14, which includes many new features to improve the overall functionality and security of the device. Among the exciting features of Android 14 is the AI improvements, which boost the ease of use while at the same time optimizing performance.

The Google Pixel 8a is designed to provide a simple, intuitive, and highly customizable software experience for users to personalize the device as they want. Google's promise of regular software updates means that even after the initial purchase, Google Pixel 8a will continue receiving the latest security patches and feature enhancements.

Connectivity and 5G on Google Pixel 8a

With Google Pixel 8a, you will enjoy 5G connectivity that allows you to download and upload files very fast, streaming will be smoother, and performance will be greatly enhanced whenever you are using data. You can be streaming movies, playing games online, or holding video conferences-you will always find a connection that is robust with the Google Pixel 8a. As 5G spreads out and becomes more pervasive, Google Pixel 8a future-proofs your device so that you'll always be connected wherever you go.

Apart from having 5G support, the Google Pixel 8a is also accompanied by Wi-Fi 6, which improves connectivity speed and stability in crowded areas such as airports, offices, and coffee shops. The Google Pixel 8a also boasts Bluetooth 5.2, supporting smooth connectivity to a wide range of wireless accessories, including headphones and smartwatches.

Security Features on Google Pixel 8a

The security feature Google is the major component in this lineup of products; it has ensured that it keeps all data safe, and the Google Pixel 8a is no exception. This device, with these various features, should give ample security. It comes fitted with an in-display fingerprint scanner that should make for easy unlocking. However, you can unlock it another way with the help of Google Pixel 8a Face unlock. With Google's advanced AI and machine learning capabilities, the Google Pixel 8a ensures that your phone remains protected from unauthorized access.

The Google Pixel 8a also offers robust privacy features, allowing you to have greater control over your data. Google's commitment to user privacy ensures that you can trust the device to keep your information safe while delivering a top-notch experience.

Conclusion

The Google Pixel 8a is an amazing smartphone that offers an unbeatable combination of performance, design, and innovation. Its sleek design, vibrant OLED display, powerful performance, and exceptional camera system make the Google Pixel 8a stand out in the crowded mid-range smartphone market. The Google Pixel 8a is that smartphone, no matter whether you're seeking a powerhouse for photography, performance with speed, or an ease of user experience. Google committed to its devices being up to date in software and to offering 5G connectivity, so it was time for Google Pixel 8a, built for the future.